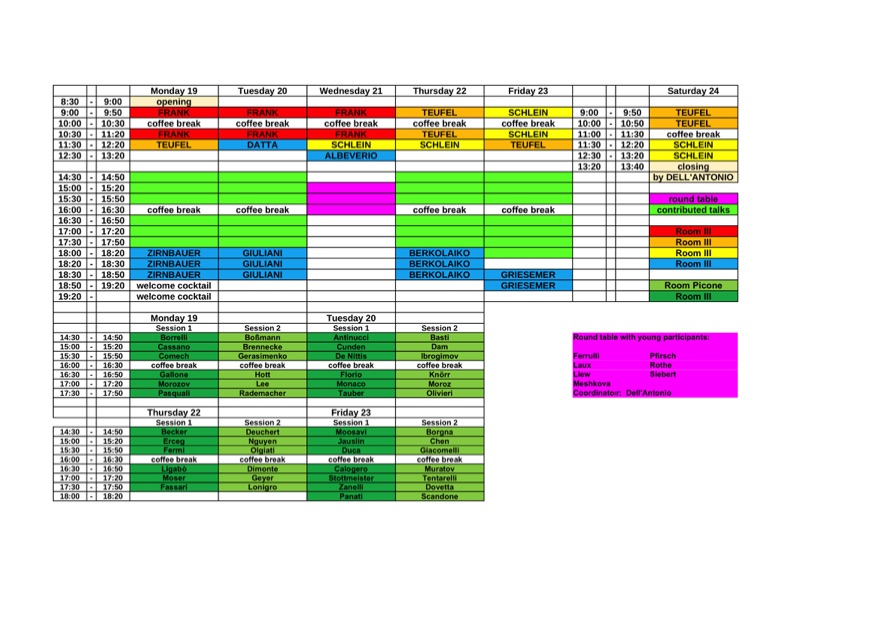
Courses

Mathematical Challenges in Quantum Mechanics

Rupert Frank (Ludwig Maximilian Universität München)

''The ionization problem''

Abstract: The ionization conjecture says that a nucleus of charge Z can bind at most Z+C electrons, where C is a constant independent of Z. (In nature, probably C=1 or C=2 will do.) This conjecture is still open. We review some results related to this problem and, in particular, Solovej’s solution of the analogous problem in Hartree-Fock theory. We also discuss some recent contributions obtained jointly with Nam and van den Bosch.

Benjamin Schlein (Universität Zürich)

"Bogoliubov theory for excitation spectra of interacting Bose gases"

Abstract: We consider systems of N interacting bosons in the Gross-Pitaevskii limit, where the scattering length of the potential is of the order 1/N and N tends  to infinity. For non-negative and sufficiently weak interactions, we establish the low-energy spectrum, i.e. the ground state energy and low-lying excitations, up to errors that vanishes in the limit of large N. As a result, we rigorously confirm the validity of Bogoliubov’s 1947 predictions.

This talk is based on joint works with C. Boccato, C. Brennecke and S. Cenatiempo.

Stefan Teufel (Universität Tübingen)

"Adiabatic theorems in quantum mechanics“

Abstract: Starting from Kato’s classical result I will discuss various developments in and applications of adiabatic perturbation theory in quantum mechanics. These developments include adiabatic theory to all orders, adiabatic theorems without spectral gap, adiabatic theorems for non-self-adjoint generators, and very recent adiabatic theorems for extended systems. Applications will be primarily from the area of solid state physics and particular emphasis will be given to geometric aspects like the role of the Berry connection.

Plenary Speakers

Sergio Albeverio (Universität Bonn)

"Quantum fields and point interactions"

Gregory Berkolaiko (University A&M of Texas)

"Local nodal surplus and nodal count distribution of graphs with disjoint loops"

Abstract: We start by reviewing the notion of "quantum graph", its eigenfunctions and the problem of counting the number of their zeros. The nodal surplus of the n-th eigenfunction is defined as the number of its zeros minus (n-1).  When the graph is composed of two or more blocks separated by bridges, we propose a way to define a "local nodal surplus" of a given block.  Since the eigenfunction index n has no local meaning, the local nodal surplus has to be defined in an indirect way via the nodal-magnetic theorem of Berkolaiko, Colin de Verdiere and Weyand.

We will discuss the properties of the local nodal surplus and their consequences.  In particular, its symmetry properties allow us to

prove the long-standing conjecture that the nodal surplus distribution for graphs with 𝛽 disjoint loops is binomial with parameters (𝛽, 1/2).

Nilanjana Datta (University of Cambridge)

"Concentration of quantum states from quantum functional and transportation cost inequalities"

Abstract: Quantum functional inequalities (e.g. the logarithmic Sobolev and Poincaré inequalities) have found widespread application in the study of the behavior of primitive quantum Markov semigroups. The classical counterparts of these inequalities are related to each other via a so-called transportation cost inequality of order 2 (T2). The latter inequality relies on the notion of a metric on the set of probability distributions called the Wasserstein distance of order 2. (T2) in turn implies a transportation cost inequality of order 1 (T1). In this paper, we introduce quantum generalizations of the inequalities (T1) and (T2), making use of appropriate quantum versions of the Wasserstein distances, one recently defined by Carlen and Maas and the other defined by us. We establish that these inequalities are related to each other, and to the quantum modified logarithmic Sobolev and Poincaré inequalities, as in the classical case. We also show that these inequalities imply certain concentration-type results for the invariant state of the underlying semigroup. We consider the example of the generalized depolarizing semigroup to derive concentration inequalities for any finite dimensional full-rank quantum state. These inequalities are then applied to derive upper bounds on the error probabilities occurring in the setting of finite blocklength quantum parameter estimation. This is joint work with Cambyse Rouzé.

Alessandro Giuliani (Università di Roma TRE)

"Universality of the Hall conductivity in interacting electron systems"

Abstract: The Haldane model is a paradigmatic 2d lattice model exhibiting the integer quantum Hall effect. We prove that for short-range interactions the Hall conductivity is quantized, for all the values of the parameters outside two critical curves, across which the model undergoes a `topological' phase transition: the Hall coefficientremains integer and constant as long as we continuously deform the parameters without crossing the curves; when this happens, the Hall coefficient jumps abruptly to a different integer. In contrast to previous work, we do not assume the interaction to be small with respect to the bare gap. The non-renormalization of the Hall conductivity arises as a simple

consequence of lattice conservation laws and of the regularity properties of the current-current correlations. Our method provides a full construction of the critical curves, which are modified (`dressed') by the electron-electron interaction. The shift of the transition curves manifests itself via apparent infrared divergences in the naive perturbative series, which we resolve by exact renormalization group methods.

Marcel Griesemer (Universität Stuttgart)

"On the 2d Fermi-polaron"

Abstract: The Fermi polaron denotes a system composed of an ideal gas of N fermions interacting with an impurity particle. The interaction between impurity and fermions is given in terms of two-body point interactions whose strength is determined by the two-body binding energy. The self-adjoint realization requires a UV regularization and the Hamiltonian emerges in the strong resolvent limit as the UV cutoff is removed. An explicit expression is not available for the Hamiltonian but for a Birman-Schwinger type operator also known as charge operator in this context. A novel variational principle relating the spectra of the Hamiltonian and the Birman-Schwinger operator opens the door to the spectral analysis of the Fermi polaron. Going through this door we prove stability of the 2d fermi polaron as well as a conjecture in the physical literature concerning the form of the ground state in the case of strong coupling.

Martin Zirnbauer (Universität Köln)

"Bott periodicity and the "periodic table" of topological insulators and superconductors"

Abstract: Bott periodicity is said to be one of the most surprising phenomena in topology. Perhaps even more surprising is its recent appearance in condensed matter physics. Building on work of Schnyder et al., Kitaev argued that symmetry-protected ground states of gapped free-fermion systems, also known as topological insulators and superconductors, organize into a kind of periodic table governed by a variant of the Bott periodicity theorem. In this talk, I will sketch the mathematical background, the physical context, and some new results of this ongoing story of mathematical physics.